Circle of Fourths with Inversions
I’ve been exploring Python and NumPy for synthesizing music. One program I wrote generates circles of fourths, with harmonic seventh chords, and inverts the chords such that all tones fall within a single octave. This gives the feeling of a never ending descent of fifths or ascent of fourths (whichever way you choose to look at it), all without actually leaving the octave range.
First, take a listen:
The Theory
The Circle of Fifths can also be thought of as a circle of fourths. So we start at A (specifically, A3 which is 220 Hz), and work our way around the circle of fifths in a counter-clockwise fashion.
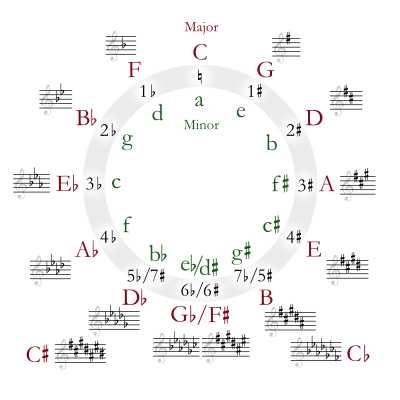
We start at A, working counter-clockwise, to D, G, and so on, until finally ending on E. Since we’ll be repeating the whole sequence, the E resolves back to the A and the process continues on. And since we’re using dominant 7th chords, we have a sense of resolution on each. A7 -> D7 -> G7 … -> E7 -> A7 … and so on.
The Code
The interesting parts of the code are below.
I used my PyWaveTools library to do the synthesis using sine waves. I set the base root note to 220 Hz which is A3. Then we build an array of NOTES to hold all the root notes we’ll be cycling through, stacking in fourths, by multiplying each by a fourth interval. Since a 4th is actually 5 semitones away, and there are 12 semitones in an octave, we use the 2*(5i/12.0) multiplier to achieve a fourth of a given tone1. We do this 11 times to get all 12 notes into the array.
import wavelib
SAMPLE_RATE = 44100.0
NOTE = 220.0 # A3
NOTES = [NOTE]
note = NOTE
for i in range(1, 12):
note = NOTE * (2**(5*i/12.0)) # equal temperament
NOTES.append(note)
I decided to play each note for one second, so we set up the total duration, and use PyWaveTools to build an array of times for the whole buffer.
NOTE_DURATION = 1 # play each n seconds
DURATION = len(NOTES) * NOTE_DURATION
times = wavelib.createtimes(DURATION, SAMPLE_RATE)
I wanted to keep all of the tones within the same octave, so I set min/max notes to constrain my frequencies to a between A3 and A4).
# keep it within one octave, so we'll invert as needed
notemin = NOTE
notemax = NOTE * 2
The intervals array holds all the intervals of each given root note we will generate. In this case, I want a Root note (1), major 3rd (5/4 interval), a perfect fifth (3/2 interval), and a harmonic seventh (7/4 interval). I am using Just Intonation intervals here to minimize the “beats”, which would be intolerable if using Equal Temperament. I chose the harmonic seventh (as opposed to a normal minor seventh interval of 9/5) to sweeten it, again reducing the beats within the chords.
I loop through each interval, so I can build a sine wave for that specific voice within the chord. I then loop through each step in the cycle of fourths, multiply or divide by 2 to get it into the desired octave range, and then set that frequency, f, to a NumPy array at the appropriate 1-second mark. Once I have the frequency array built, I generate the sine wave for that voice. Each voice/harmony sine wave is simply added to the final vals array to build the chord.
# use harmonic 7th (7/4 interval) for smoother beatless chord
intervals = [1.0, 5.0/4.0, 3.0/2.0, 7.0/4.0]
vals = wavelib.zero(times)
for i in range(len(intervals)):
interval = intervals[i]
freq = wavelib.zero(times)
for n in range(len(NOTES)):
note = NOTES[n]
f = NOTES[n] * interval
while f >= notemax:
f = f / 2.0
while f < notemin:
f = f * 2.0
startidx = int(n * NOTE_DURATION * SAMPLE_RATE)
endidx = int(((n+1) * NOTE_DURATION) * SAMPLE_RATE)
freq[startidx:endidx] = f
vals += wavelib.sinewave(times, freq)
And finally, we normalize the wave values to get it to a consistent gain, then use the play_n function to play the sequence a total of 5 times. This gives us a full 60 seconds of cycling fourth chords.
vals = wavelib.normalize(vals)
vals = wavelib.play_n(vals, 5)
wavelib.write_wave_file('output/circle_fourths_chords.wav', vals)
The full source code is available in the PyWaveTools repo, specifically this file: circle_fourths_chords.py
Notes
1.: My algorithm originally used the stacking of perfect fourth intervals (4/3 ratio, about 498 cents) to build the circle, as opposed to equal temperament of 500 cents (using the (2*(5i/12.0)) multiplier). Thus by the end where we wrap from E7 to back around to the beginning of the next A, the interval was a little off. It is barely noticable, but I decided to correct it. You can hear the original in the following clip… notice when it wraps from E back to the A (every 12 seconds) the jump feels just slightly off.